代码随想录10 动态规划

动态规划基础

什么是动规？

动态规划，英文：Dynamic Programming，简称DP，如果某一问题有很多重叠子问题，使用动态规划是最有效的。

动规问题的特点是每一个状态一定是由上一个状态推导出来的，这是与贪心的重要区别（贪心不推导状态，直接选取局部最优解）

解题步骤

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

LeetCode 509 斐波那契数

力扣题目链接(opens new window)

斐波那契数，通常用 F(n) 表示，形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是： F(0) = 0，F(1) = 1 F(n) = F(n - 1) + F(n - 2)，其中 n > 1 给你n ，请计算 F(n) 。

示例 1：

• 输入：2
• 输出：1
• 解释：F(2) = F(1) + F(0) = 1 + 0 = 1

示例 2：

• 输入：3
• 输出：2
• 解释：F(3) = F(2) + F(1) = 1 + 1 = 2

示例 3：

• 输入：4
• 输出：3
• 解释：F(4) = F(3) + F(2) = 2 + 1 = 3

提示：

• 0 <= n <= 30

暴力方法

如果输入的n大于2，就逐个累加，得到长度为n+1的斐波那契数列数组，返回最后一个数即可

var fib = function(n) {
    let dp = [0, 1]
    for(let i = 2; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2]
    }
    console.log(dp)
    return dp[n]
};

动规

状态转移方程为：dp[i] = dp[i-1] + dp[i-2]，因此只需要两个变量记录状态

var fib = function(n) {
    // 动规状态转移中，当前结果只依赖前两个元素的结果，所以只要两个变量代替dp数组记录状态过程。将空间复杂度降到O(1)
    let pre1 = 1
    let pre2 = 0
    let temp
    if (n === 0) return 0
    if (n === 1) return 1
    for(let i = 2; i <= n; i++) {
        temp = pre1
        pre1 = pre1 + pre2
        pre2 = temp
    }
    return pre1
};

LeetCode 647 回文子串

力扣题目链接(opens new window)

给定一个字符串，你的任务是计算这个字符串中有多少个回文子串。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

示例 1：

• 输入：”abc”
• 输出：3
• 解释：三个回文子串: “a”, “b”, “c”

示例 2：

• 输入：”aaa”
• 输出：6
• 解释：6个回文子串: “a”, “a”, “a”, “aa”, “aa”, “aaa”

提示：输入的字符串长度不会超过 1000 。

暴力解法

先找到所有子串，然后判断每个子串是否是回文串，复杂度O(n^3)

var countSubstrings = function (s) {
    let count = 0
    for (let index = 0; index < s.length; index++) {
        for (let end = index; end < s.length; end++) {
            let str = s.substring(index, end + 1)
            count++
            for (let flag = 0; flag < str.length / 2; flag++) {
                if (str[flag] != str[str.length - 1 - flag]) {
                    count--
                    break
                }
            }
        }
    }
    return count
};

动态规划

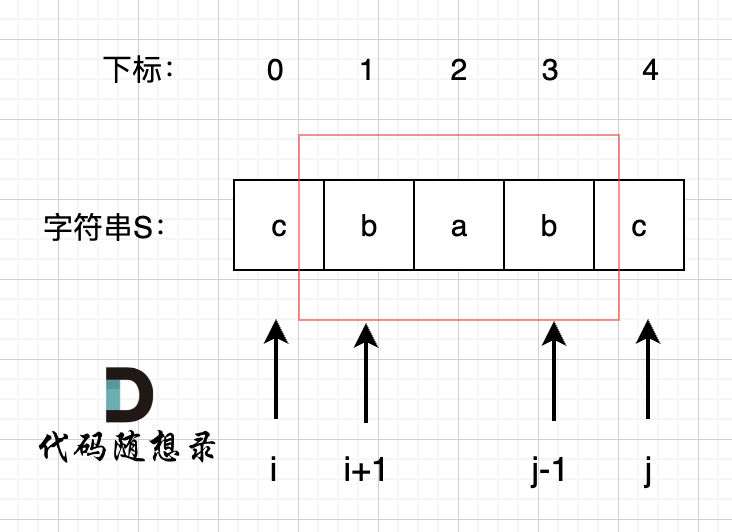
分析可知，要判断字符串 d[i][j] 是否为回文子串，可以先看 d[i+1][j-1] 是否为回文串；

接下来确定递推公式：

如果 d[i] != d[j]，则d[i][j] 一定不是回文子串

如果 d[i] == d[j]，分两种情况：

​ 当 j-i <= 1 时，d[i][j] 是回文子串

​ 当 j-1 > 1时，如果 d[i+1][j-1] 是回文子串，则 d[i][j] 是回文子串

递归公式如下：

if (s[i] == s[j]) {
    if (j - i <= 1) { // 情况一 
        result++;
        dp[i][j] = true;
    } else if (dp[i + 1][j - 1]) { // 情况二
        result++;
        dp[i][j] = true;
    }
}

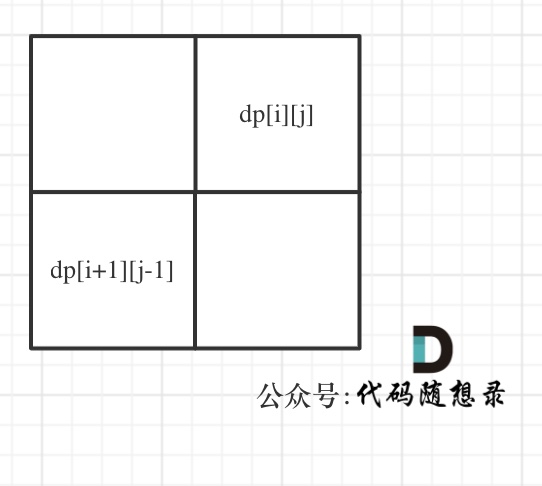
所以，可以将回文子串映射到二维数组上，如果对应位置为true，则是回文子串，如果为false，则不是;

先将所有 d[i][j] 初始化为 false，不能在初始化时就完成判断；

根据递推公式，d[i][j] 是根据其左下角的 d[i+1][j-1] 得到的，因此在遍历时应当从下往上，从左往右遍历

const countSubstrings = (s) => {
    const strLen = s.length;
    let numOfPalindromicStr = 0;
    let dp = Array.from(Array(strLen), () => Array(strLen).fill(false));

    for(let j = 0; j < strLen; j++) {
        for(let i = 0; i <= j; i++) {
            if(s[i] === s[j]) {
                if((j - i) < 2) {
                    dp[i][j] = true;
                } else {
                    dp[i][j] = dp[i+1][j-1];
                }
                numOfPalindromicStr += dp[i][j] ? 1 : 0;
            }
        }
    }

    return numOfPalindromicStr;
}

LeetCode 70 爬楼梯

力扣题目链接(opens new window)

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

• 输入： 2
• 输出： 2
• 解释： 有两种方法可以爬到楼顶。
  • 1 阶 + 1 阶
  • 2 阶

示例 2：

• 输入： 3
• 输出： 3
• 解释： 有三种方法可以爬到楼顶。
  • 1 阶 + 1 阶 + 1 阶
  • 1 阶 + 2 阶
  • 2 阶 + 1 阶

var climbStairs = function(n) {
    // dp[i] 为第 i 阶楼梯有多少种方法爬到楼顶
    // dp[i] = dp[i - 1] + dp[i - 2]
    let dp = [1 , 2]
    for(let i = 2; i < n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2]
    }
    return dp[n - 1]
};

Leetcode 746 使用最小花费爬楼梯

力扣题目链接(opens new window)

旧题目描述：

数组的每个下标作为一个阶梯，第 i 个阶梯对应着一个非负数的体力花费值 cost[i]（下标从 0 开始）。

每当你爬上一个阶梯你都要花费对应的体力值，一旦支付了相应的体力值，你就可以选择向上爬一个阶梯或者爬两个阶梯。

请你找出达到楼层顶部的最低花费。在开始时，你可以选择从下标为 0 或 1 的元素作为初始阶梯。

示例 1：

• 输入：cost = [10, 15, 20]
• 输出：15
• 解释：最低花费是从 cost[1] 开始，然后走两步即可到阶梯顶，一共花费 15 。

示例 2：

• 输入：cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
• 输出：6
• 解释：最低花费方式是从 cost[0] 开始，逐个经过那些 1 ，跳过 cost[3] ，一共花费 6 。

提示：

• cost 的长度范围是 [2, 1000]。
• cost[i] 将会是一个整型数据，范围为 [0, 999] 。

var minCostClimbingStairs = function (cost) {
    let dp = [0, 0]
    for (let i = 2; i <= cost.length; i++) {
        if ((dp[i - 1] + cost[i - 1]) > (dp[i - 2] + cost[i - 2])) {
            dp[i] = dp[i - 2] + cost[i - 2]
        } else {
            dp[i] = dp[i - 1] + cost[i - 1]
        }
    }
    return dp[cost.length]
};

Leetcode 62 不同路径

力扣题目链接(opens new window)

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

• 输入：m = 3, n = 7
• 输出：28

示例 2：

• 输入：m = 2, n = 3
• 输出：3

解释： 从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

示例 3：

• 输入：m = 7, n = 3
• 输出：28

示例 4：

• 输入：m = 3, n = 3
• 输出：6

提示：

• 1 <= m, n <= 100
• 题目数据保证答案小于等于 2 * 10^9

var uniquePaths = function (m, n) {
    let dp = new Array(m).fill(0).map(() => new Array(n).fill(0))
    dp[0][0] = 1
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n ; j++) {
            if (i == j && i == 0){
                continue
            }
            let top = 0;
            let right = 0;
            if (i - 1 >= 0) {
                top = dp[i-1][j]
            }
            if (j - 1 >= 0) {
                right = dp[i][j-1]
            }
            dp[i][j] = top + right
        }
    }
    console.log(dp)
    return dp[m-1][n-1]
};