数据结构01-并查集
并查集(Union-Find)
基本定义:
并查集是指:对集合有“并”和“查”两种操作的一种数据结构;(这里的集合可以理解为无向图)
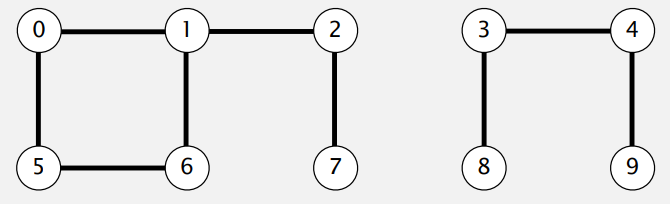
并操作:将两个节点连通;
查操作:两个节点是否是连通的;
连通性:
自反性:p 与 q 连通 即 p 被与 q 连通
对称性:p 与 q 连通,则 q 与 p 连通
传递性:如果 p 连通 q,q 连通r,则 p 连通 r
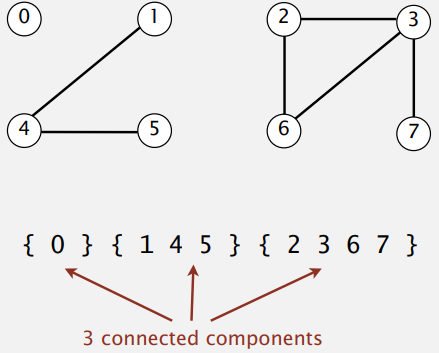
连通子图:
相互连通的最大集合,例:
实现操作:
对于一个有 N 个节点的并查集,可能有 M 个“并”或“查”的操作混合使用,实现操作的目的是当 N 和 M 非常大的时候仍让保持”并“和”查“高效,
思路1:快速查找
思路:使用大小为 N 的数组存储连通关系,当且仅当数组中的两个值相等时,其下标所指的节点是连通的;初始化时,每个节点的原始值即为本身;
例:
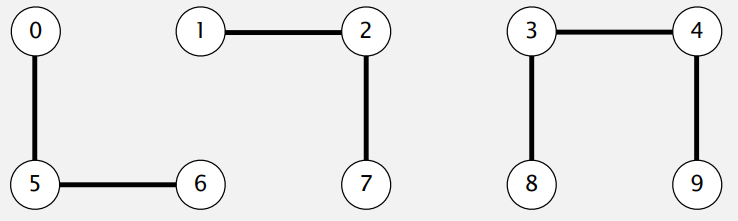

这种思路下,很容易进行查找操作,对于节点 i 和节点 j,只需要比较 id[i] 和 id[j] 的值,相等则连通,不相等则不连通,时间复杂度为 O(1)。
但在进行“并”操作时代价较高,如果要连接 p 节点和 q 节点,不仅需要将其将 q 点的值修改为 p 点的值,还需将所有与 q点 的值相等的节点的值都修改为 p 点的值,这需要对整个数组进行一次遍历,时间复杂度为 O(N)。

思路2:快速合并
思路:这一思路采用树形结构来存储,同样使用大小为 N 的数组,但存储的是节点的父节点,初始化时,每个节点的原始值即为本身;
例:
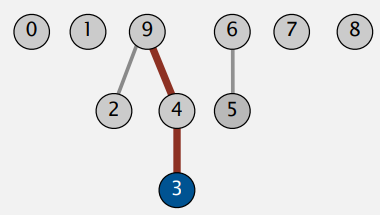

这种思路下,很容易进行连接操作,对于节点 p 和节点 q,只需要将 q 的值修改为 p 的值(q的父节点为q)即可,时间复杂度为 O(1);
但在进行“查找”操作时代价较高,要判断两节点是否连通,需要判断两节点是否有相同的“根”
如要比较 2 号 和 3 号节点,需要先找到 2 的根节点:2 的父节点是 9, 9 的父节点是 9 本身,所以 2 的根节点为 9;再寻找3的根节点:3 的父节点是 4, 4 的父节点是 9, 9 的父节点是 9 本身,所以 3 的根节点也为 9;因此两者是连通的。
在寻找时,需要逐层向上寻找父节点,最坏情况下,如果整个并查集是一个深度为 N 的树,则时间复杂度达到 O(N)
改进思路1:加权快速合并
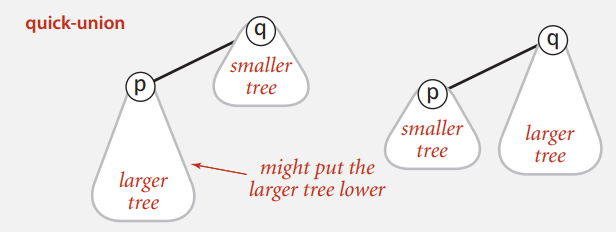
思路:快速合并的问题在于,树的深度过高会影响查找速度,那么可以通过优化树的高度来改进:
快速合并在进行连接操作时,如要将 p 和 q 连接,由于总是将 p 连接到 q,可能将更高的树的父节点设置为更矮的树,这使得树的高度被进一步增高;
如果能够记录树的深度,每次连接时都能将更矮的树的父节点设置为更高的树,就能缩短树的高度。
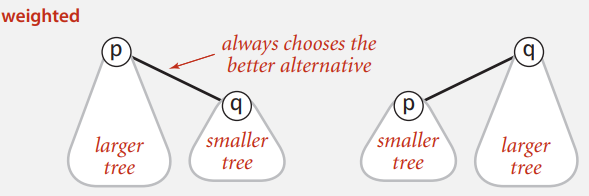
在实现时,需要额外增加一个数组,用于记录根为 i 的树中的节点数目,增加了一定的空间开销(空间换时间);
改进思路2:路径压缩
思路:仍然通过优化树的高度来改进:
路径压缩优化不在连接的时候进行,在查找操作时进行:当查询到某节点的根节点时,直接将节点的父节点设置为根节点,缩短了字树的高度,在下次查找时就能节省时间了;
例:查询 9 的根节点时,需要逐层查询 9、6、3、1 的父节点,其根节点都为 0,则将这些点的,父节点都设置为 0
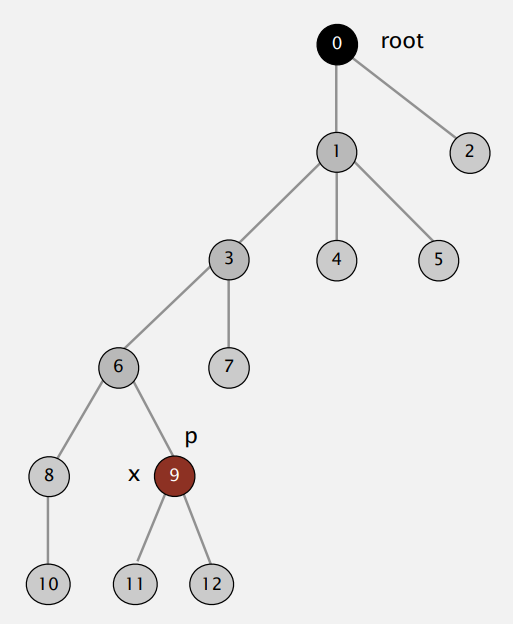
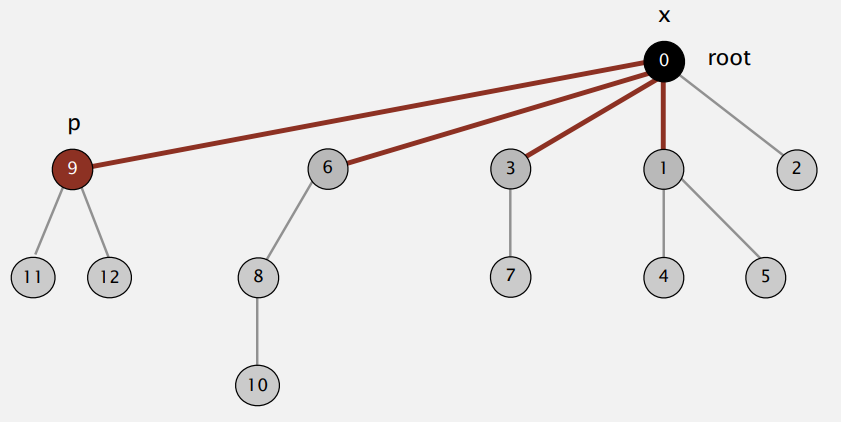
这一操作使得树变得“扁平”,且不增加时间复杂度(只需要一个额外的赋值操作)
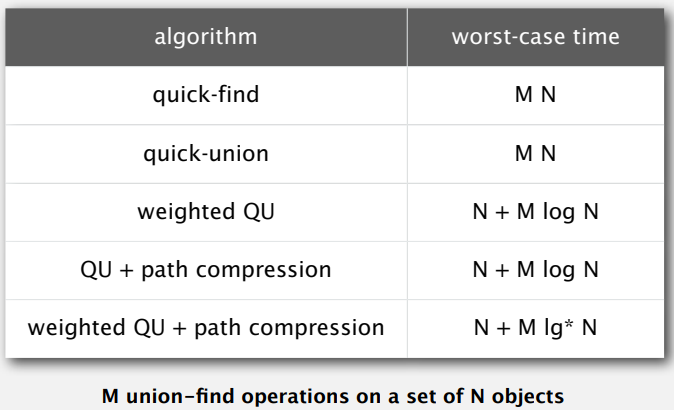
总结:时间复杂度分析