形式语言与自动机04-NFA

如果要构建一个在字母表 {0, 1}上的，接受以 101 为结尾的字符串的 DFA，答案如下：

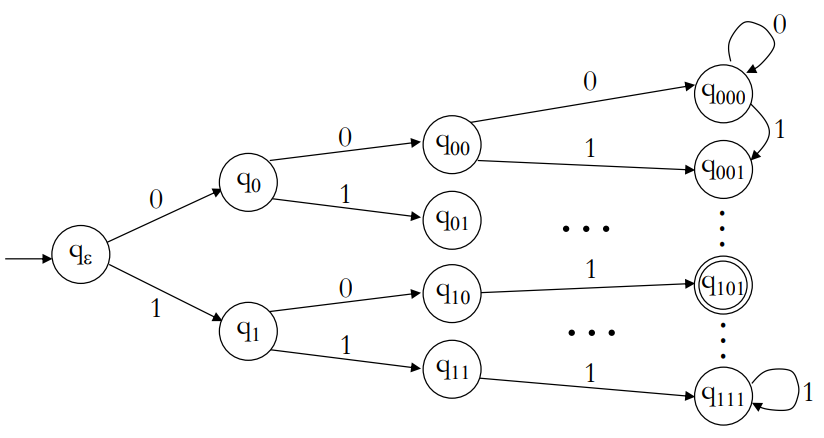
假设我们可以猜测我们正在读取的字符串何时只剩下3个符号，那么我们可以简单地寻找序列101，如果我们看到它就接受它

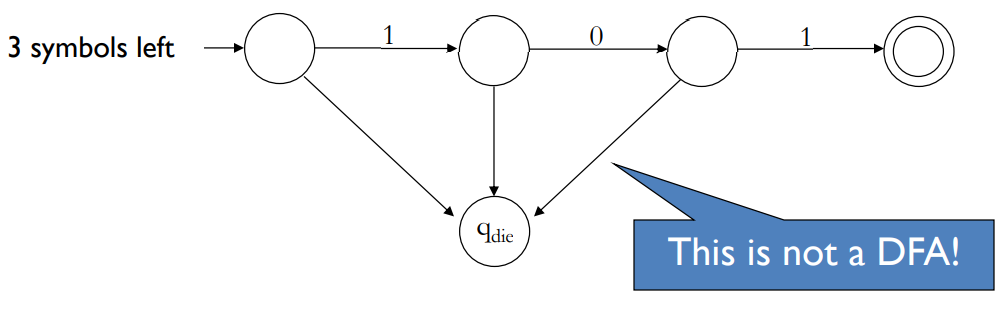
由于你无法确定什么时候字符串快要结束，这一自动不再具有确定性

这种非确定性是一种猜测的能力，我们可以稍后验证

以 101 结尾的字符串语言的非正式化的非确定性算法：

1. 猜测你是否接近输入的结束
2. 如果猜测为是，寻找101并且当看到他的时候接受
3. 如果猜测为否，再读入一个字符串并跳转到一步

非确定有限自动机 Nondeterministic finite automata

这时一种允许你进行猜测的自动机，例如：

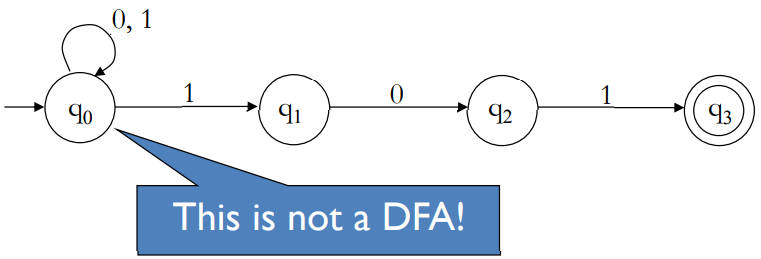
• NFA 的每个状态可以有 0 个、1 个或多个用相同符号标记的跃迁
• 状态 $q_0$ 有两个标记为 1 的跃迁
• 当读到 1 时，我们可以选择保持 $q_0$ 还是移动到 $q_1$
• 状态 $q_1$ 没有标记为 1 的跃迁
• 在 $q_1$ 读入 1 时，就“死掉”了；读入 0，继续到 $q_2$
• 状态 $q_3$ 没有向外的跃迁，当在 $q_3$ 读入任何字符时，也会“死掉”

NFA 由五个元组组成：

• $Q$ 是有限的状态集合
• $\Sigma$ 是字母表
• $ \delta : Q \times \Sigma \to Q$的子集，是转移函数
• $q_0 \in Q$ 是初始状态
• $F \subseteq Q$ 是接受状态的集合（最终状态，在图表中用双圈表示）

只在 $ \delta $ 上和DFA有区别，$ \delta$ 是一个状态集合

下面是一个 NFA 的图例：

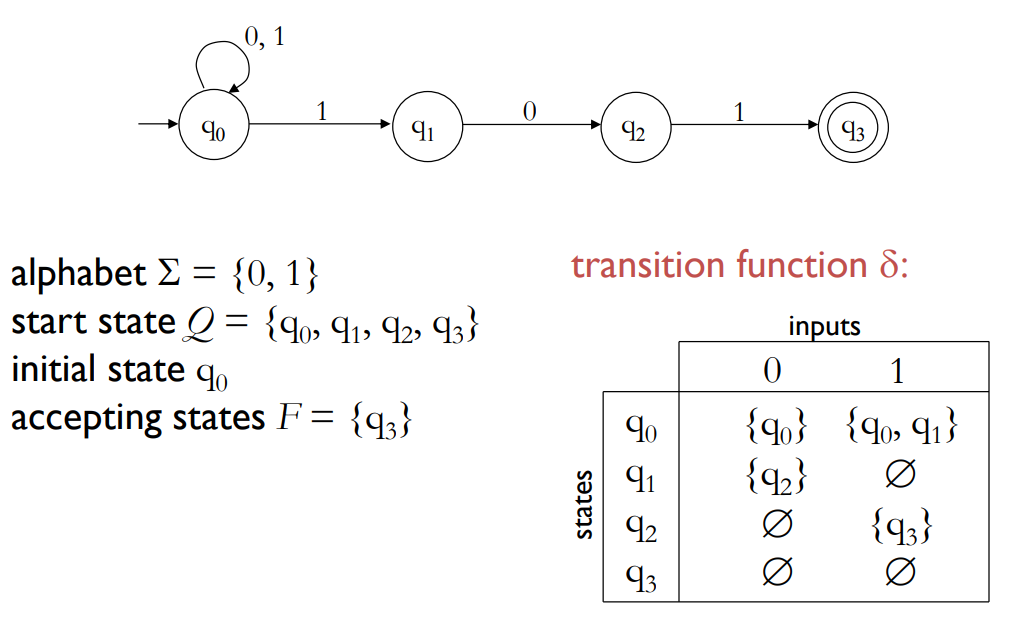
NFA 的语言：

NFA 的语言是所有字符串的集合，其中存在某种路径，从初始状态开始，当字符串从左向右读取时，该路径将导致接受状态。

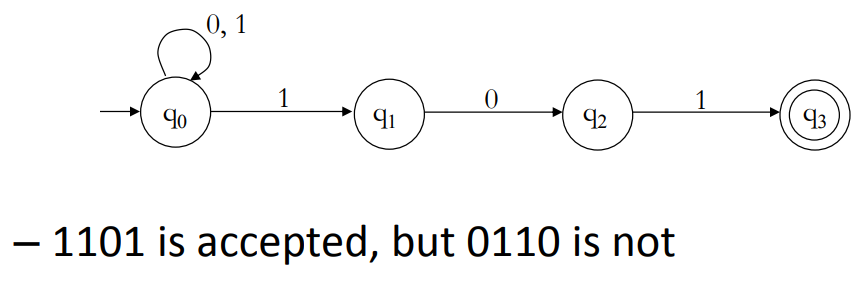
NFA 可以做到一切 DFA 可以做到的事，但它不能做更多。

语言 L 如果可以被一些 DFA 接受，那么它一定可以被一些 NFA 接受。