形式语言与自动机03-DFA

有限自动机 Finite Automata

一个有限自动机的例子

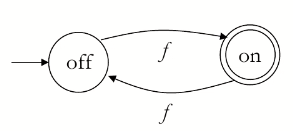
这是第一节课中给出的单开关灯泡电路的案例，这个例子中，有“开”和“关”两个状态，自动机的初始状态是“关”，并且尝试到达“好状态”——“开”。

那么要经历什么样的 f 操作序列才能到达好状态呢？

答案是：${ f, fff, fffff, …} = {f ^n:n \ is \ odd }$

这是一个在字母表${f}$上的特定有限自动机的例子。

确定有限自动机 Deterministic finite automata

DFA 由五个元组组成：

• $Q$ 是有限的状态集合
• $\Sigma$ 是字母表
• $ \delta : Q \times \Sigma \to Q$，一个转移函数
• $q_0 \in Q$ 是初始状态
• $F \subseteq Q$ 是接受状态的集合（最终状态，在图表中用双圈表示）

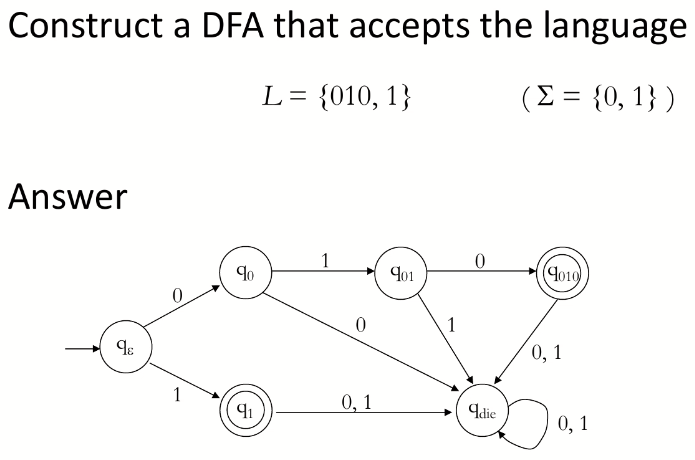
下面是一个 DFA 的图例：

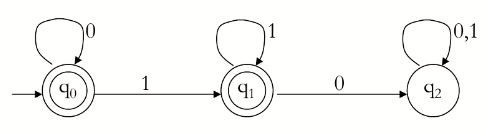
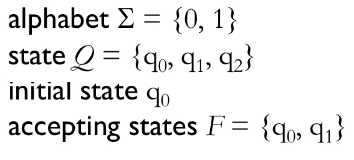
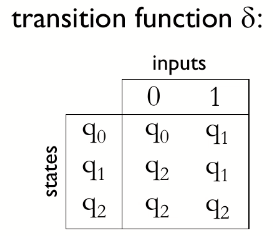
DFA 的语言：

一个 DFA 的语言是在其字母表 Σ 上的字符串的集合，且若按照字符串顺序从左到右执行转化操作，可以从初始状态开始到达某个结束状态。