形式语言与自动机02-字母表和字符串
字母表和字符串
将词语、数字、词组等表示成字符串是一种常用方式,要定义字符串,就需要字母表;
字母表是一个有限且非空的符号集合,例:

字母表 Σ 上的字符串是一个 Σ 中符号的有限序列,空字符串表示为ε,例:
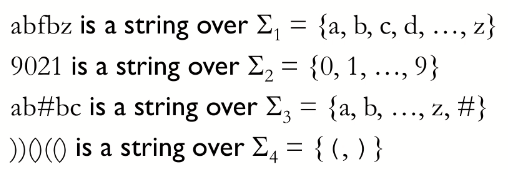
语言是字母表上的字符串的集合,语言可以用于表示有 “YES/NO” 答案的问题;

字母表总是有限的,而语言总是无限的(有限语言的研究价值太低);
基于以上思想,我们将计算问题转化为集合归属问题来解决,例如:
一个计算问题为:数字 x 是素数吗?
可以转化为: $ x \in PRIMES = {2,3,5,7,11,13,17,…} ?$
这里的 PRIMES 是一种语言, 是由字母表 $ \Sigma_2$ 中的字符串中的素数形成的语言;
字符串操作
Concatenation 串联,无符号,直接连写即可
$$
w = a_1a_2…a_n &abba\
v = b_1b_2…b_m &bbbaaa\
wv=a_1a_2…a_nb_1b_2…b_m &abbabbbaaa
$$
Reverse 翻转,右上角 R,翻转字符串
$$
w = a_1a_2…a_n &abbab\
w^R=a_n…a_2a_1 &babba
$$
Length 取长度,绝对值符号,获取字符串长度
$$
w = a_1a_2…a_n &abba\
|w|=n &4
$$
对于空集 ε
$$
|\epsilon| = 0 \
\epsilon w = w\epsilon = w \
\epsilon abbac = abb \epsilon ac = abbac\epsilon = abbac
$$
Substring 子字符串,一个连续字符的子序列

Prefix 前缀,Suffix 后缀,一个字符串可以分解为前缀和后缀两部分

Exponent 指数操作,即重复 n 次
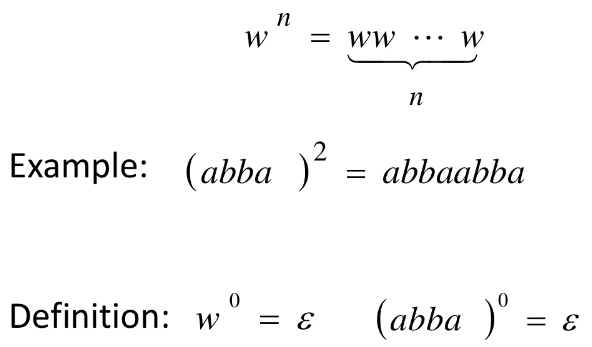
* 操作,得到所有可能的字符串,总是无限的
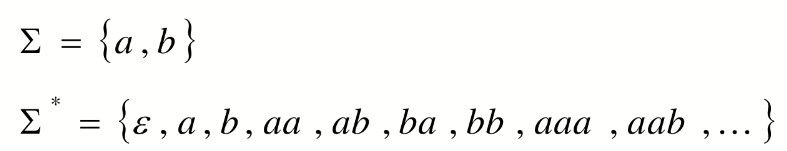
+ 操作,得到除空集外的所有可能字符串,总是无限的
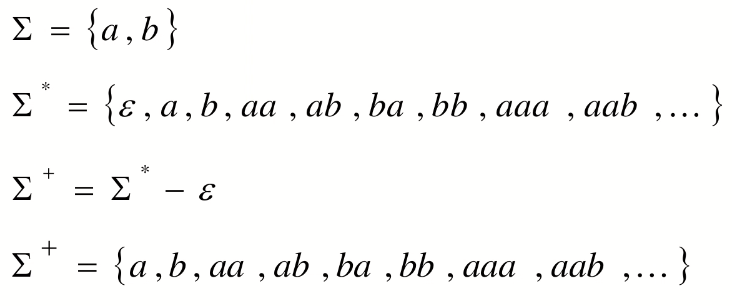
现在我们可以得到语言的集合定义,即 任何一个在字母表 Σ 上的语言,都是 Σ* 的子集;
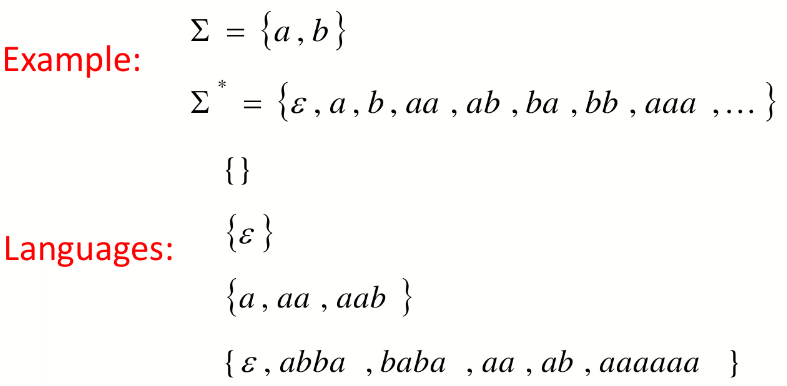
注意,空集也是一种语言,只有空字符串的集合也是语言;且这二者大小不同;

由于有限语言的研究价值较低,我们考虑无限的语言,如:

这里的语言 L 表示 a 的 n 次幂与 b 的 n 次幂的串联
语言操作
由于语言是一种集合,我们可以使用所有集合操作:
交、并、差:
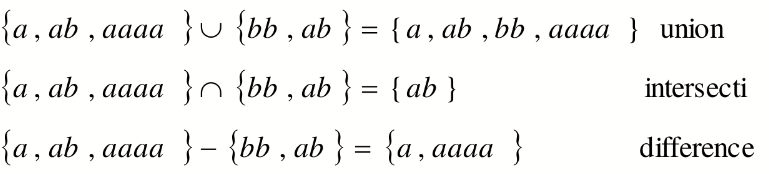
补:
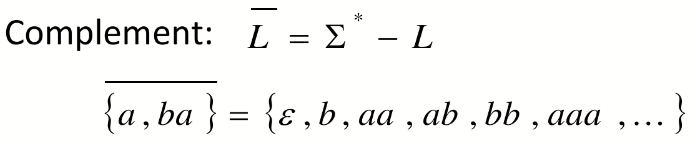
Reverse 翻转:
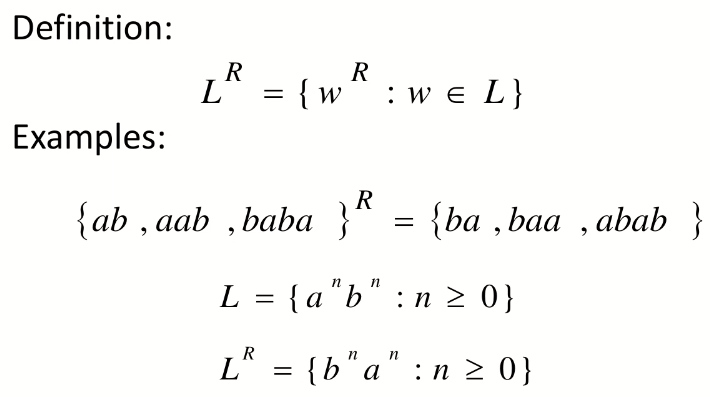
串联:
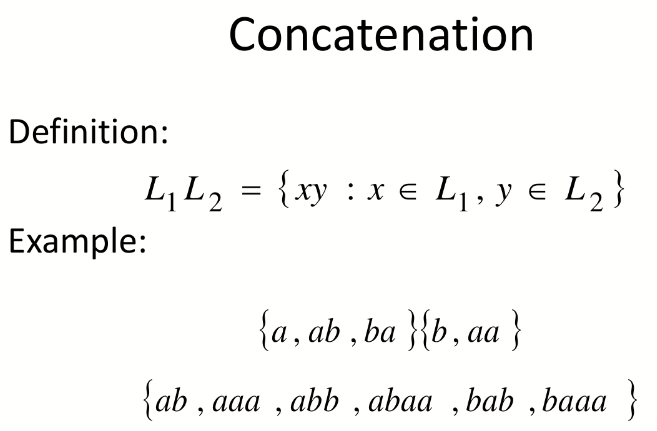
注意,如果 L1 或 L2 为空集,连接的结果也为空集
幂次:
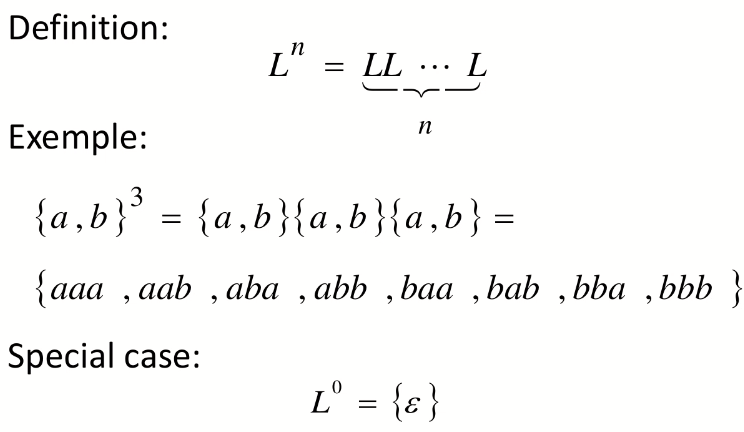
Star-Closure ( Kleene *)
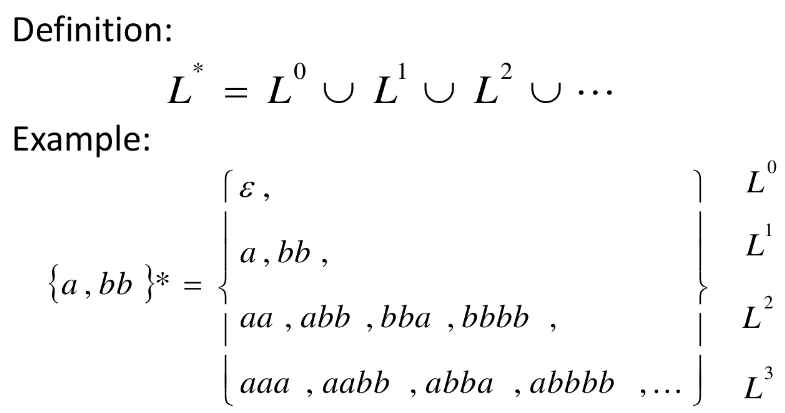
Positive closure (+)
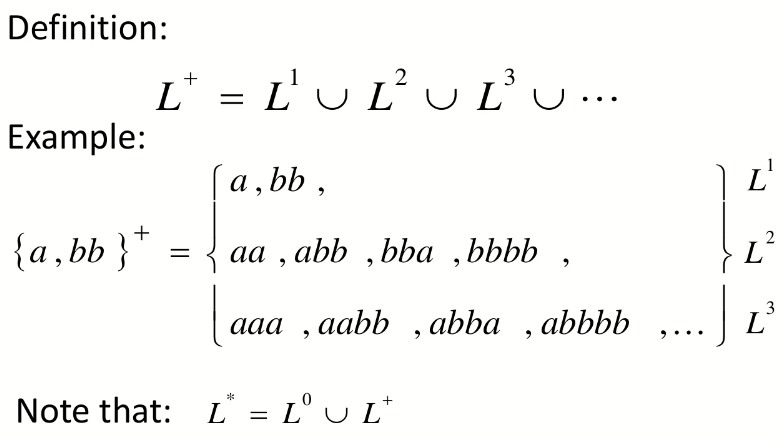
注意这里不能写为 L+ = L* - ε,如果 L 中本身就有 ε,则会出错