形式语言与自动机01-自动机理论

什么是自动机理论？

• 自动机理论是抽象计算设备（真实计算机的简化抽象模型）的研究
• 抽象模型可以帮助我们理解计算机，了解我们能用计算机做什么、做不了什么

一个简单例子

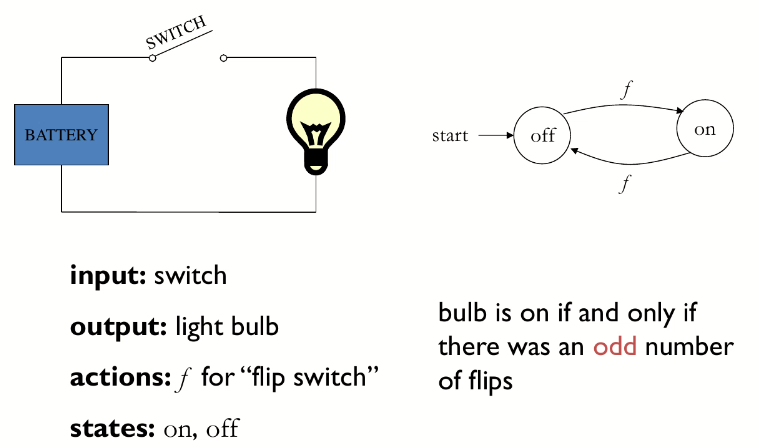
左图可以视为一个简单计算机系统，以开关信号作为输入，以灯泡作为输出，唯一的操作是“拨动开关，那么整个系统只存在两个状态：灯开和灯关；

该系统可以抽象为右侧的模型，并将初始状态设为灯关的情况，抽象为这样的模型后，我们可以直观的看到，当操作 f 执行奇数次的时候，灯是开启状态，执行偶数次则是关闭状态；

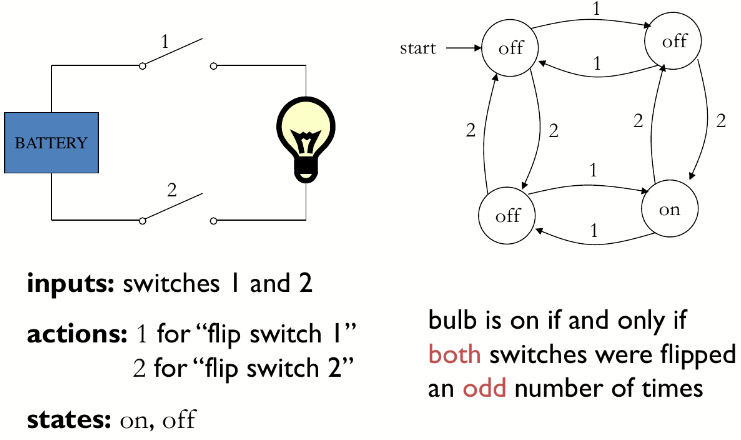
当存在两个开关时，情况变得复杂了，抽象为右侧模型后，我们可以发现：只有两个开关都拨动奇数次时，灯才会是开的

如果要设计一个电路系统， 使得当且仅当所有开关拨动相同次数时，灯会开启，如何设计系统？

这样的复杂问题就需要更加强大的模型抽象能力去解决了，也就是自动机理论要解决的问题：我们能不能设计出这样的系统？如何设计这样的系统？

这些抽象模型可以用来描述许多小型计算机系统，比如微波炉或闹钟的控制组件；

这些模型同样也应用于词法分析器中，用于辨别编程语言的表达式是否正确，如：

// is a legal name of a variable in c
int ab1;

// is not
int 5u=;

不同种类的自动机

上述的只是一种计算机设备，还有很多其他的种类：

自动机	内存	使用范围
finite automata 有限自动机	设备内存有限；	用于建模小型计算机；
push-down automata 下推自动机	设备内存无限，以受限形式访问；	用于建模解析器等；
Turing Machines 图灵机	设备内存无限；	用于建模任何计算机；
time-bounded Turing Machines 有界图灵机	设备内存无线，但限制运行时间；	用于建模任何以“合理”时间运行的计算机程序

本课程学习前两者：

有限自动机：我们将学习有限内存的设备可以做什么，不可以做什么；介绍“模拟”：一个设备模仿另一个设备的能力；介绍“不确定性”：设备做出任意选择的能力；

下推自动机：与语法有关的设备，描述了编程语言（以及自然语言）的结构；

图灵机：是计算机的通用模型，计算出我们希望能计算的任何事物，；

问题

我们要形式化的问题一定是有：”Yes/No” 回答的问题， 比如：

• 给定一个词语，是否含有给定的另一个词缀；
• 给定一个数 n ，能否被 7 整除？
• 给定一个含有括号的表达式，每个左括号都有与之匹配的右括号吗？

这种问题中只有确定答案，不会出现：“寻找xxx”，“有多少xxx”的问题，这些问题我们暂不考虑