机器学习01 介绍

台大李宏毅老师机器学习课程学习笔记，重新整理：

Machine Learning ≈ Looking for Function

简单来说，机器学习的实质是寻找一个难以用人力创造的函数

如下图：

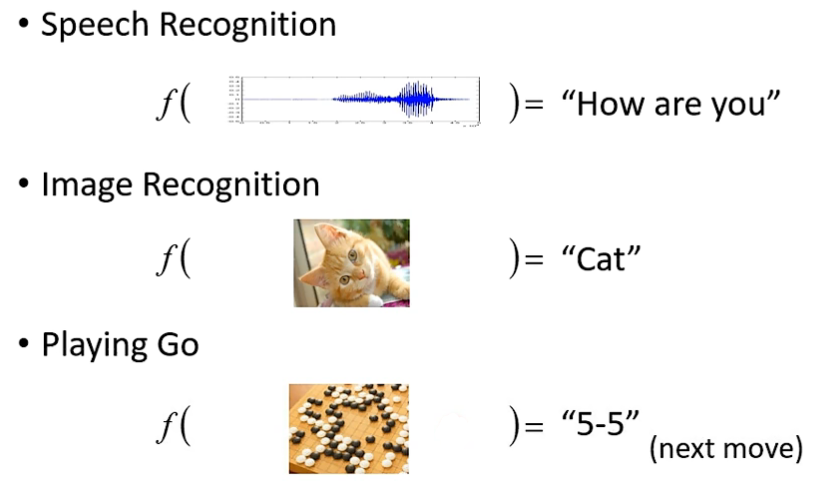
很多复杂问题都能概括为寻求一个函数，给定输入，以期望得到某个正确的输出。

• 语音识别：给定音频信号，输出对应语言的文字
• 图像识别：给定图片数据，输出对应事物的名称
• 围棋AI：给定棋盘数据，得到胜率最高达的下一步坐标

但这些问题通常难以解决，特别是涉及高维和低维信息之间转换的问题，难以用传统方法寻求二者之间的联系。

随着计算机算力水平的提升，用机器每秒上百万次的强大运算能力来“暴力破解”输入输出之间的关系也不再是空谈，这就是机器学习。

机器学习的分类

简单来说机器学习可以分为以下三类：

Regression（回归）：让函数得到某个数值。如 PM2.5 预测

Classification（分类）：给出一些选项（类别），函数输出正确的选项。如垃圾邮件分类

Structured Learning（结构）：构建出具有结构的输出。如生成图像，文档

如何获得这个函数？

函数由表达式、输入和输出组成，第一步就是写出表达式：

1.写出带有未知参数的函数

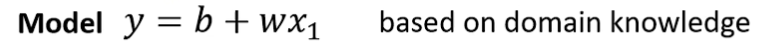
其中，y是函数结果，x1是输入。

通常而言，我们不表达式都不是上图这种简单的线性方程，具体函数形式基于不同的问题而定，上面的例子中，习惯将w称作权重，b称作偏差。

如何选择合适的表达式，构建出符合问题要求的模型，是当下机器学习领域的重点之一。

不难看出，上述表达式中存在很多未知的参数，这些参数就是要求解部分，得到参数后，对于任意给定的输入均能得到对应输出。

那么参数如何计算得到呢？

要计算参数，可以通过对已知结果逆运算得出，这些已知的“输入”被称为特征，“输出”被称为标记，共同构成了训练数据。

如果有海量的训练数据，就能通过这些数据反推出合适的参数，从而得到最终的表达式。为此需要有一个衡量参数好坏的函数，在每一次使用训练数据计算参数时，对参数进行评估，从而方便下一步对参数进行调整。

2.基于训练数据计算 Loss

Loss 是计算结果偏差的函数，用于衡量当前得到的未知参数的好坏。

在第一次计算时，我们可以随机对参数进行赋值，将输入代入表达式，得到预测结果，之后与 Label（真实数据） 计算Loss（通常是MAE、MSE等差额计算）。从而反映出本次表达式所使用的的参数的优劣程度。

如果将各种可能的未知参数都尝试一遍，计算出相应的 Loss，绘制出 ”Error Surface“，可以观测到最合适的未知参数。

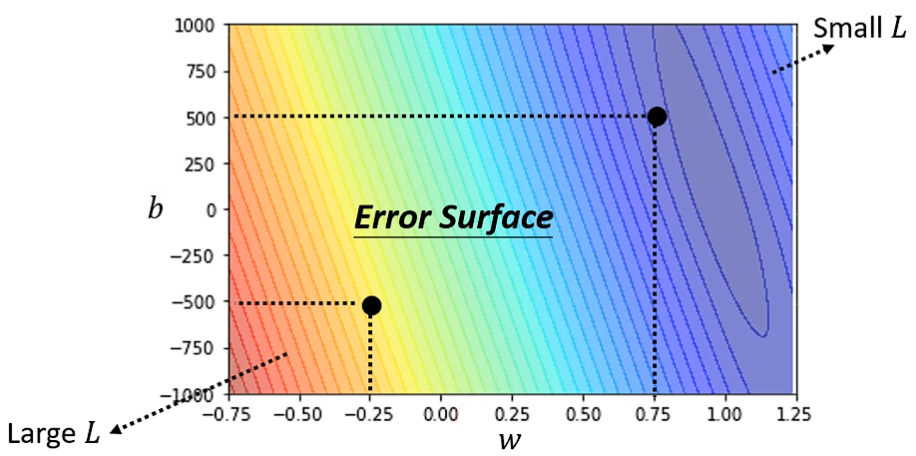
但真实情况中，由于参数众多，形式复杂，很难用图像直观表达出来，只能得到不同情况下参数对应的 Loss 值。

在得到 Loss 后，我们就了解了目前的参数的优劣，之后就需要将参数进行调整，使计算结果更加贴近真实值，让 Loss 越来越小，也就是 Optimization（优化） 的过程。

3.优化

获得最佳的未知参数，可以使用 Gradient Descent（梯度下降） ，单个参数的该算法步骤如下：

首先，随机选取一个 w 作为初始值

其次，计算该 w 对应的 loss 值，并计算 L 在 w 上的微分（即斜率）

​ 通过这一步，我们可以确定此时的 w 值是偏大还是偏小，如果斜率为正，说明 w 增加会增大 Loss，w 减少则会减少 Loss，斜率为负值则相反，

之后，我们需要设定一个 η（学习速率），来划定我们每次对 w 的变化大小， 对 w 进行变化（用 η 乘上微分）后反复如上的计算，从而获得最佳的未知参数。这些由我们自己设定的参数被称为 Hyperparameters（超参数）

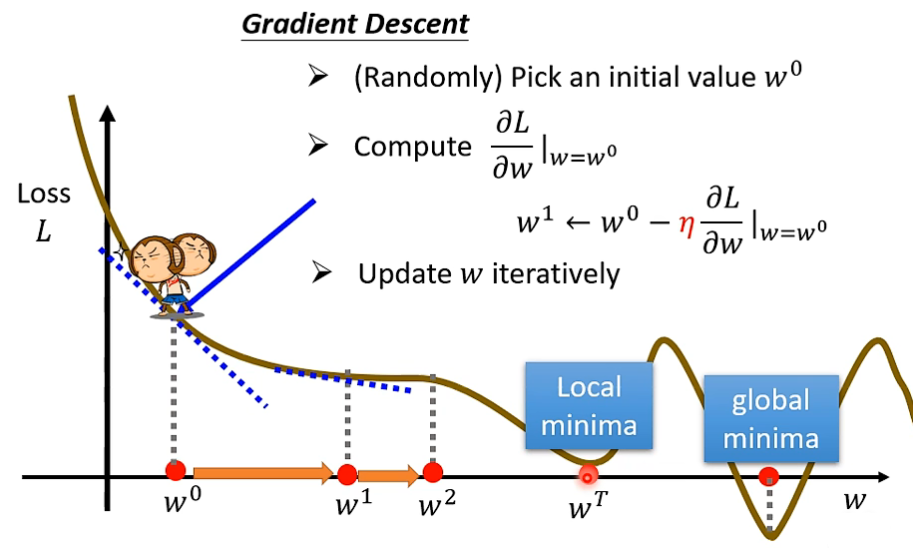
然而，我们很容易发现，这种方法在微分值为0时就会停止，得到的参数可能只是局部最佳值，而非全局最佳值。不过尽管 Gradient Descent 存在这一问题，但在实际生产实践中可以通过取多次随机点的方式轻松解决，这一方法的真正痛点另有别处。

相应的，多参数方法也很容易得到：

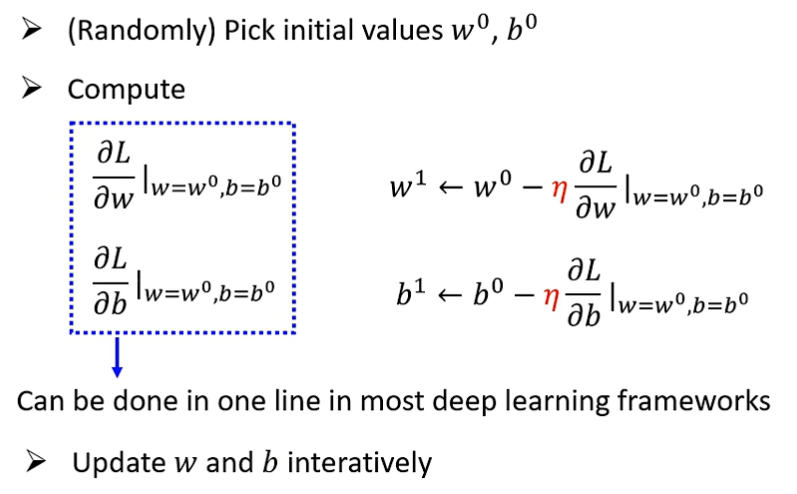
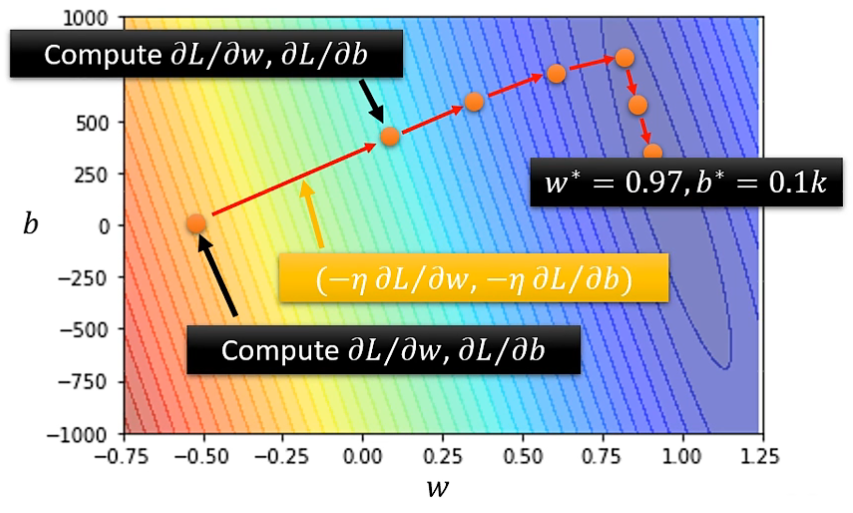
如何改进？

经过上述的三个基本步骤，我们很容易就能计算出“最佳”的未知参数，但事实上，这种预测往往存在较大偏差，在上述例子中，我们选用的是最简单的 Liner Model（线性模型），即使用权重和偏差值来进行预估的简单模型，这种模型考虑的因素少，性能有限，只能表现线性的单调变化。

实际问题中，我们往往需要更加贴合实际问题的模型，这才是机器学习的难点所在。

Sigmoid Function（S形函数）

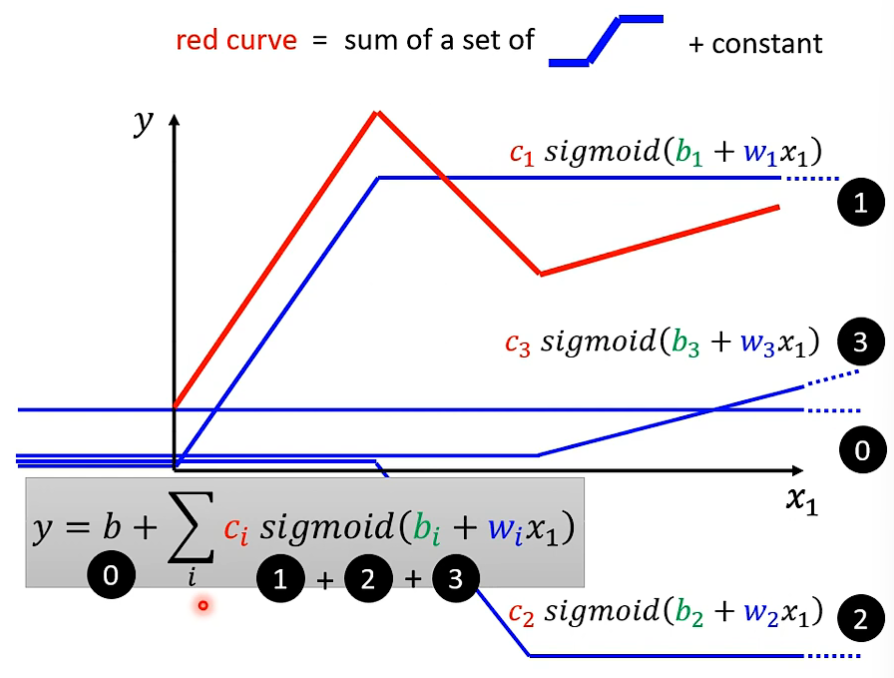
由于函数变化多种多样，我们可以将函数分为多段，每一段视为一个斜率近似固定的直线，这样我们就将一条曲线分解为了多段曲线之和，每一段曲线的其他部分均为常数，只有在与其斜率吻合的部分是有斜率的，即下图的 Hard Sigmoid（硬S函数）

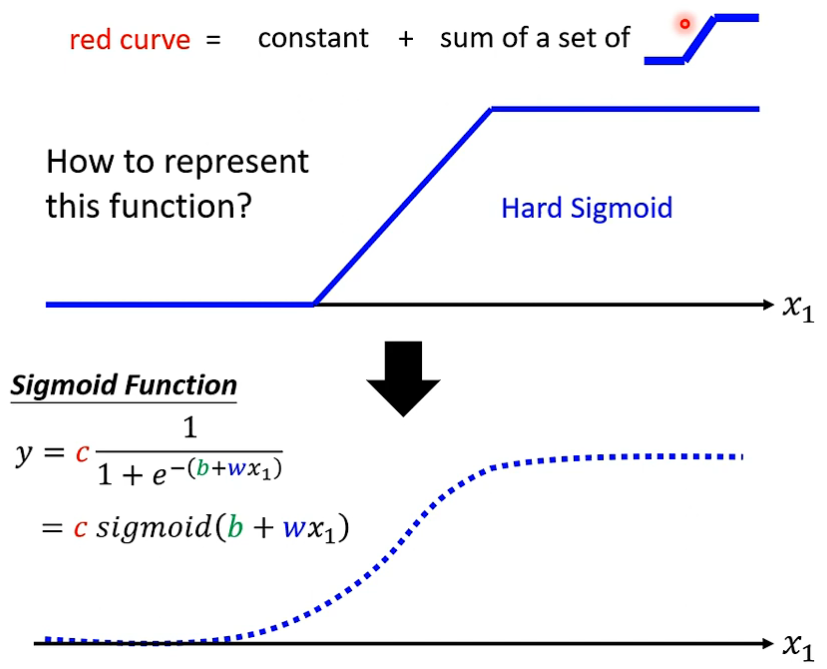
由于分段函数表达式不便于计算，我们使用 Sigmoid Function（S形函数）来近似的表达这些曲线。

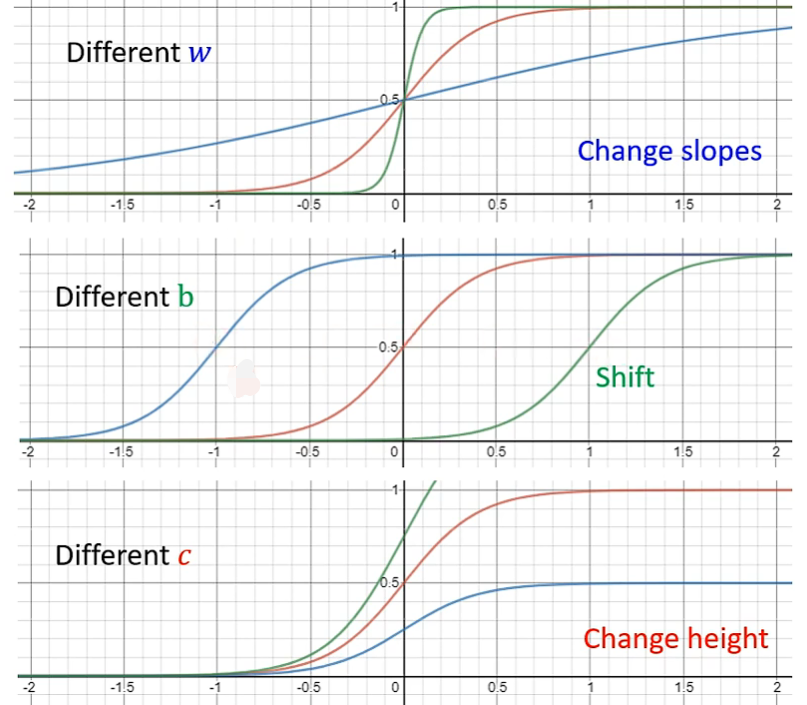
其中，w 用于改变斜率，b 用于改变左右位置，c 改变高度

这样我们就能将曲线拆分为多个 Sigmoid Function 之和：

将这一程序化过程用线性代数表示即为如下方式：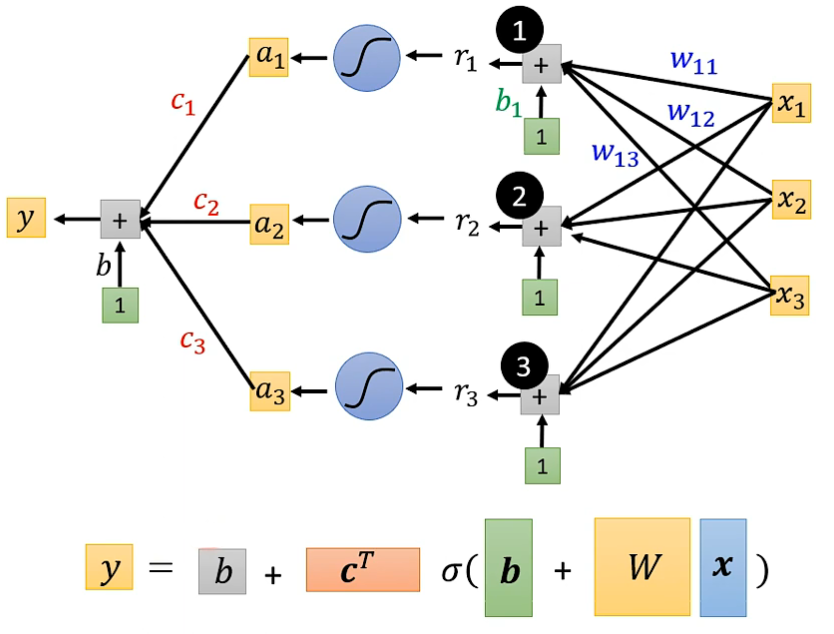

将其中的未知参数拼接为向量 θ ：

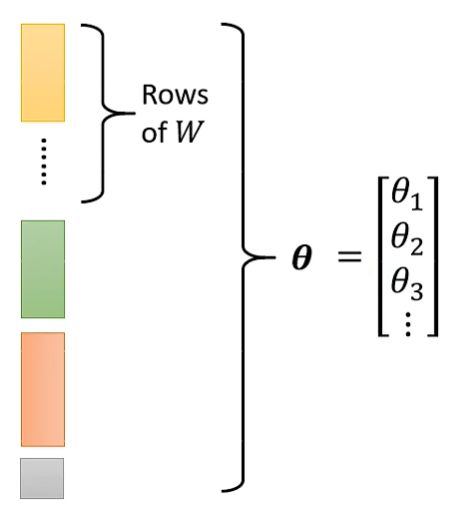
此时，Loss 计算方法不变，仍然是给定一组 θ ，与真实值 label 进行对比即可：

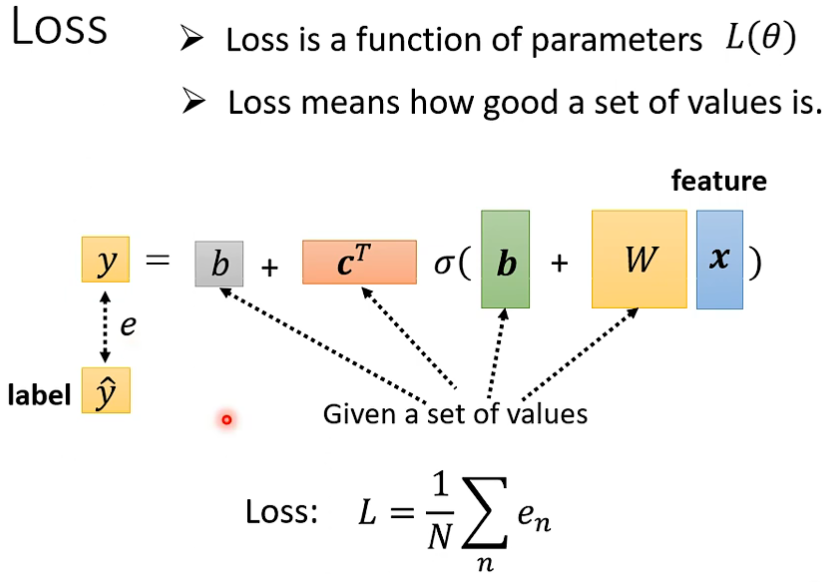
参数优化方法也仍然相似：

​ 找出初始值（随机）；

​ 求参数向量的微分向量（ gradient ）；

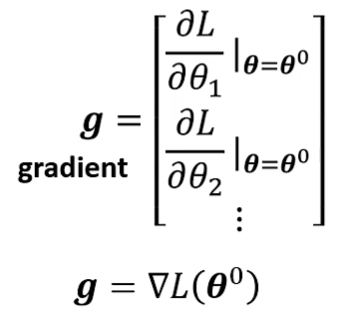
​ 更新 θ 向量：

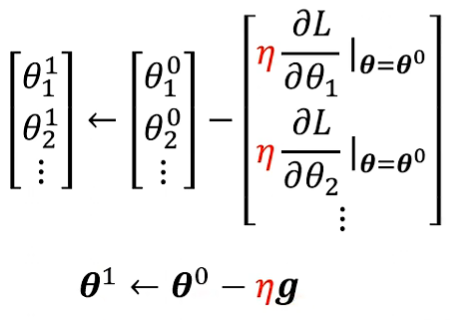
重复计算和更新，直到计算结束（无法计算或重复一定次数）

分组（Batch）优化

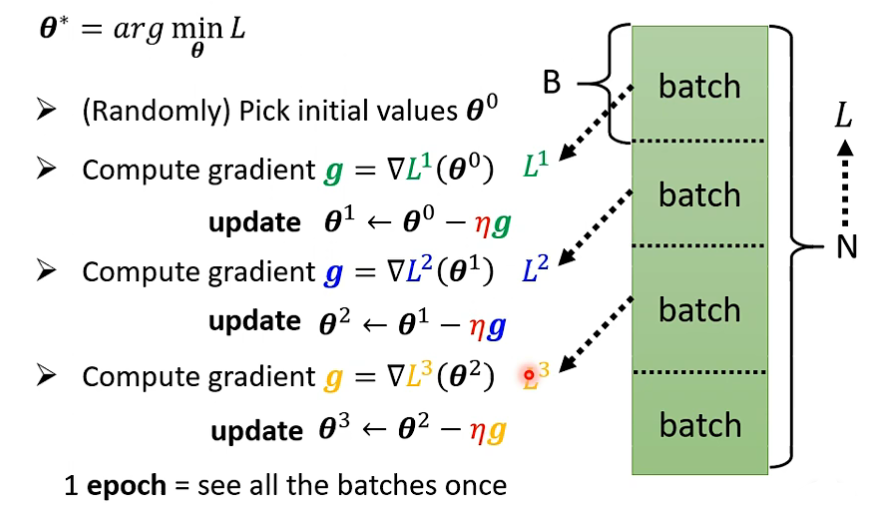
之前计算 Loss 时，我们将全部输入与真实值对比得到 Loss，另一种方法是，将整个数据集分为一个个 Batch，每个 Batch 大小相同，具体大小随意。

每次对一个组进行 Loss 计算，之后使用这个 Loss 计算 gradient，使用这个 gradient 更新参数向量 θ，再将这个新的 θ 放到 下一个组中计算 Loss，如此重复直到所有的组完成一次计算，这样就对所有数据完成了一次训练，即一次 Epoch。

在这一次 epoch 中，更新了相当于 batch 数量的 update 次数。

Rectified Linear Unit（ReLU函数)

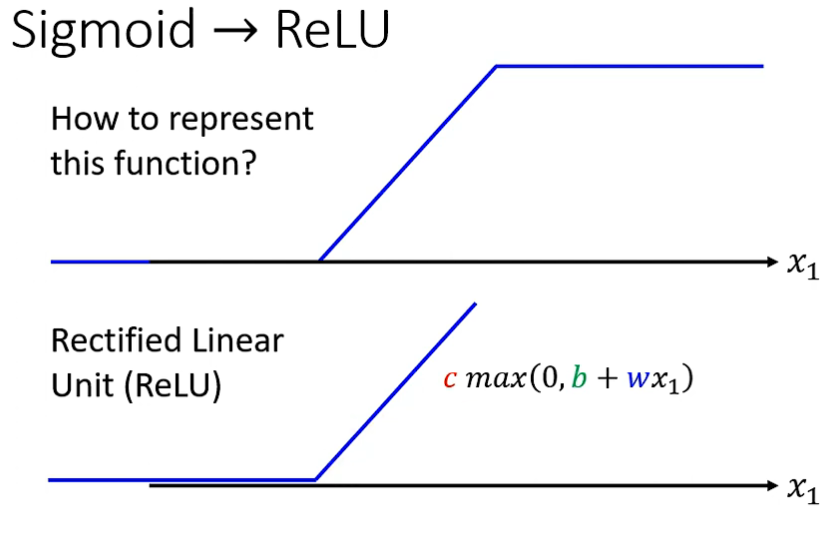
除了 S 形函数外，也可以使用上图所示的 ReLU 函数 ，两个 ReLU 函数相加就能得到一个 S 形函数表示的折线：

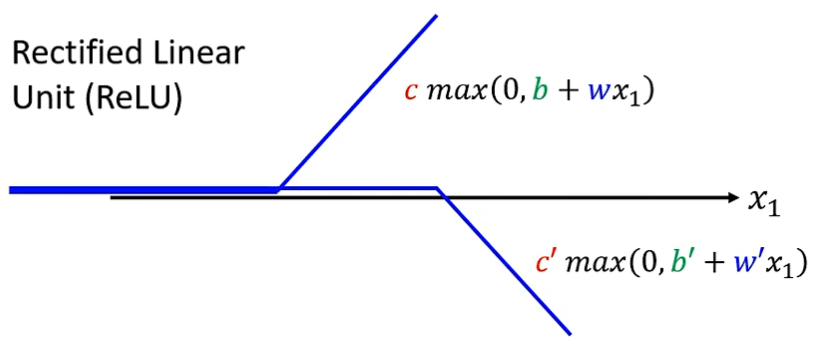
在列出表达式时需要注意：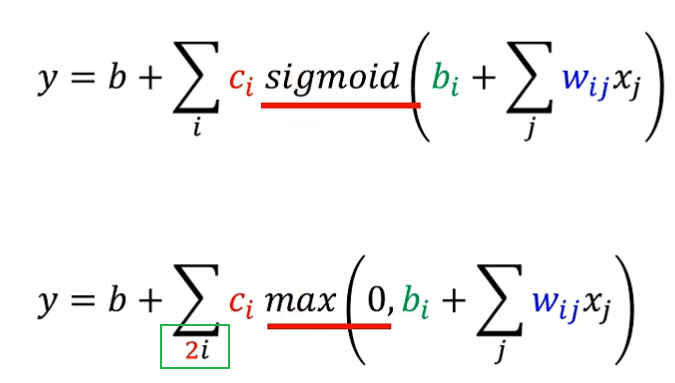

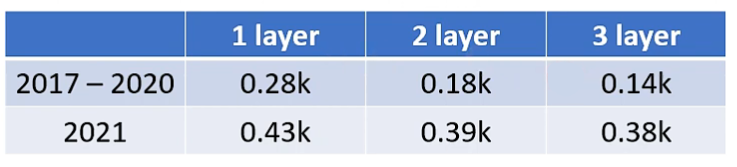
相较于线性模型，使用 ReLU 可以带来较为显著的提升，课程样例的结果如下：

可以看到当 ReLU 数量较少时效果一般，但当 ReLU 数量较多时，更加贴合的曲线就能带来更好的预测效果。

“套娃”

我们也可以使用 ReLU 等模型进行反复“套娃处理”，多进行几层，增加更多的参数，进行更相似的拟合，得到更好的预测效果：

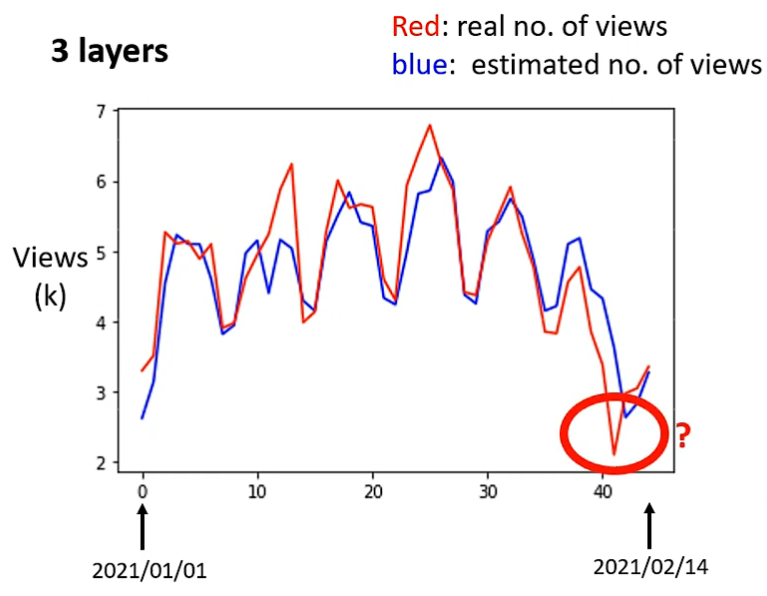
经过上述优化，我们得到的曲线如下图蓝色曲线所示，尽管已经非常贴近，但一些意外（如下图拟合失误的部分，正处于除夕，计算机无法预测到这一影响）

神经网络 & 深度学习

由于整个计算过程中有大量的 Sigmoid 或者 ReLU 这样的小单元，就好像一个个神经元一样，我们将每个 Sigmoid 或者 ReLU 称为 Neuron（神经元），整个模型被称为 Neural Network（神经网络）

像上文提到的“套娃”一样，有着多层嵌套结构的机器学习，就称为 Deep Learning 深度学习

问题：

1.既然任何曲线都可用多段的 ReLU 或 Sigmoid 拼接，为什么不使用更多的神经元来模拟，而进行这种增加层数的操作呢？

2.层数越多越好吗？然而现实中，经常出现 Overfitting（过拟合）问题，即训练资料上表现好，但在预测中表现不好，那我们该采用多少层的模型呢？又如何解决 Overfitting 问题呢？

（事实上，大所数有更多层次的模型表现不好的问题根源在于最优解没有找到，由于梯度下降方法往往只能得到局部最优解，所以产生了更差的效果，并非过拟合的情况）