论文阅读01 知识表示学习研究进展

知识表示学习研究进展论文笔记
1.知识库
现实世界中,知识是蕴藏在无(半)结构的信息中的,比如:
人工智能(Artificial Intelligence),英文缩写为AI。它是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。
这句话中蕴含着人工智能这一学科的基本定义,但这些知识是非结构化的,其中一条可以提取为:

从现实世界中的无(半)结构的信息中提取结构化的知识,就是知识库的任务。知识库将知识表示为**实体(entity)间的关系(relation)**,将人类知识经过系统组织后形成结构化知识系统。作为人类知识的结晶,知识库是推动人工智能和信息服务发展的重要基础技术。
不难看出,知识表示是知识获取与应用的基础,因此,知识表示学习问题是贯穿知识库构建于应用全过程的关键问题。
知识库通用表示方式为三元组,即(实体1,关系,实体2)的形式,对应两个有某种关联的实体。实体可以是人名、地名、机构名、概念等,关系可以是包含、等价等关系。
但这种网络形式的知识表示面临两大问题:
- 计算效率问题:这种表示方法在计算语义及推理关系时需要设计专门的图算法,有较高复杂度和较差的可拓展性,知识库较大时计算效率低,难以满足实时计算需求。
- 数据稀疏问题:由于知识库遵循长尾效应,在长尾部分存在严重的数据系数问题,且只有极少知识或路径涉及它们,对这些实体的语义或推理关系计算准确率极低。
2.表示学习
为了解决上述问题,可以使用基于深度学习的表示学习技术,将研究对象的语义信息转化为稠密的低维向量,用向量之间相对位置的远近来表示语义相似度,这样就可以高效的计算实体间语义关系,有效解决数据稀疏问题。
知识库中的 实体$e$ 和 关系$r$ 可以通过表示学习得到对应向量 $l_e$ 和 $l_r$,之后可以通过计算欧氏距离或余弦距离的方式计算语义相似度。
此前常用的独热表示的方法构建词袋模型,独热向量之间相互正交,无法计算欧氏距离或余弦距离,丢失大量语义信息。且独热表示存在严重的数据稀疏问题,特别是在语言表示中。而表示学习向量维度较低,有利于提高计算效率,缓解数据稀疏问题
表示学习是分布式的,即孤立地看向量中的一维没有明确意义,要综合各维度才能表示对象的语义信息。这一点与人脑神经元的原理相似,这里不做过多展开。表示学习也是层次结构的,这与物质的组成结构原理相似,即大的物体一般由更小的单位组成(多个维度组成表示某含义的向量)。
在构建知识图谱时,往往需要不断补充实体间关系,利用表示学习方法,可以预测两实体之间的关系,即知识图谱补全(Knowledge graph completion)
此外,由于现实生活中同一知识体系可能在不同知识库中被记录,但在不同知识库中存在不同的表示方式,难以使用传统方法融合,如果能使用表示学习方法,将多个知识库中的知识用同一方法表示出来,就能更高效的进行多知识库的有机融合,实现异质信息融合。
3.表示学习主要方法
将知识库表示为 $G=(E,R,S)$,其中 $E = {e_1,e_2,…,e_{|E|}}$ 表示实体集合,包含 $|E|$ 种不同实体,$R = {r_1,r_2,…,r_{|R|}}$ 是关系集合,包含 $|R|$ 种不同关系,$S \in E \times R \times E$ 表示三元组集合,单个三元组表示为 $(h,r,t)$,即头实体,关系,尾实体,如(史蒂夫·乔布斯,创始人,苹果公司)
3.1 距离模型(Structured Embedding, SE)
每个实体用 $d$ 维的向量表示,所有实体投影到同一个 $d$ 维的向量空间中。
每个关系 $r$ 都有两个矩阵 $M_{r,1}, M_{r,2} \in R^{d \times d}$,分别用于头实体和尾实体的投影操作。
损失函数为:
$$
f_r(h,t)=|M_{r,1}l_h - M_{r,2}l_t|
$$
可以看出,损失函数使用关系矩阵将实体投影到同一空间,之后计算距离,从而反映在r下的语义相关度,距离越小则越存在这一关系。
SE将知识库中的三元组作为学习样例,以实体向量和关系矩阵为参数,不断优化,从而实现知识表示。
缺点:使用两个不同矩阵对头尾投影,协同性差。
3.2 单层神经网络模型(Single Layer Model, SLM)
SLM 使用单层神经网络改进 SE,对每个三元组定义评分函数:
$$
f_r(h,t) = u^T_r g(M_{r,1}l_h + M_{r,2}l_t)
$$
其中 $u^T_r$ 为关系的表示向量。
SLM 使用 $g()$ 这一 $tanh$ 双曲正切函数的非线性操作来视图寻找实体与关系间的联系。
缺点:SLM的非线性操作仅提供微弱联系,却带来较高计算复杂度。
3.3 能量模型(Semantic Matching Energy, SME)
语义匹配能量模型将每个实体和关系使用低维向量表示,同时定义投影矩阵用于刻画实体与关系间的内在联系,即定义两个评分函数:
$$
f_r(h,t)=(M_1l_h + M_2l_r + b_1)^T(M_3l_t + M_4l_r + b_2)
$$
$$
f_r(h,t)=(M_1l_h \otimes M_2l_r + b_1)^T(M_3l_t \otimes M_4l_r + b_2)
$$
使用了四个投影矩阵,分别使用线性相加形式和哈达玛积的形式,再增加偏置向量,从而提高模型复杂度。
3.4 双线性模型(LFM、DistMult)
隐变量模型(Latent factor model,LFM)使用基于关系的双线性变化来刻画实体与关系之间的联系。评分函数为
$$
f_r(h,t)=l^T_hM_rl_t
$$
其中 $M_r$ 为 $r$ 对应的双线性变换矩阵(连续空间和离散空间之间转化的一种映射方法),相较于以往模型,LFM 使用简单有效的方法刻画出实体和关系间的语义联系,计算复杂度低。
DistMult 模型将 LFM 的 $M_r$ 设为对角阵,进一步简化计算的同时,模型效果得到显著提升。
3.5 张量神经网络模型(Neural Tensor Network)
用双线性张量取代传统神经网络中的线性变换层,在不同维度下降头尾实体向量连接起来。
NTN 为每个三元组定义的评分函数如下:
$$
f_r(h,t) = u^T_r g(l_hM_Rl_t + M_{r,1}l_h+M_{r,2}l_t+b_r)
$$
这一评分函数计算两个实体间存在关系 $r$ 的可能性。其中 $u^T_r$ 是与关系相关的线性层,$g()$ 为 $tanh$ 函数,$M_r$为三阶张量,$M_{r,1},M_{r,2}$为投影矩阵。可以看出 SLM 即为 NTN 的张量层数为0时的简化版本。
此外,NTN 中的实体向量为实体中所有单词向量的均值,由于实体单词数量远小于实体数量,可以重复利用单词向量构建实体表示,降低稀疏性问题,同时增强不同实体间的语义联系。
NTN引入张量操作,能更精准地刻画实体与关系之间的复杂联系,但计算复杂度非常高,需要大量训练数据。且实验表明,NTN在大规模稀疏知识图谱上效果较差。
3.6 矩阵分解模型
RESACL 模型将知识库的三元组构成一个大的张量 $X$,如果三元组 (h, r, t) 存在,则 $X_{hrt} = 1$,否则为0,之后通过张量分解的方式,将三元组对应张量值 $X_{hrt}$ 分解为实体和关系表示,使 $X_{hrt}$ 尽可能接近 $l_hM_rl_t$
实际上,RESACL 与前面的 LFM 相似,但 RESACL 也会优化值为0的位置,而 LFM 只优化存在的三元组。
3.7 翻译模型
受 word2vec 等模型展现的平移不变现象(词向量能够捕捉形如 king 和 queen、man 和 woman 之间的隐含语义关系)启发,TransE 模型被提出。
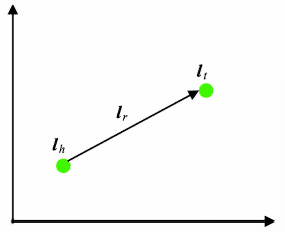
TransE 将知识库中关系看做平移向量,对每个三元组 (h, r, t),使用关系 r 的向量 $l_r$ 作为头实体向量和尾实体相连之间的平移,也可看作从头实体到尾实体的翻译,因此 TransE 也被称作翻译模型。
TransE 希望,对于每个三元组,有:
$$
l_h + l_r \approx l_t
$$
因此,TransE 定义如下损失函数:
$$
f_r(h,t)=|l_h + l_r - l_t|_{L_1/L_2}
$$
即计算向量 $l_h + l_r$ 和 向量 $l_t$ 的 $L_1$ 或 $L_2$ 距离。
相较于以往的模型,TransE 使用较少的参数,以较低的计算复杂度构建出实体与关系间的复杂联系,性能提升显著,且在大规模稀疏矩阵上表现惊人。
TransE 也面临一些问题:
- 由于 TransE 结构简单,难以除杂知识库中形如 N-N 的多对多复杂关系。相关解决方案有 TransH、TransR、TransD、TransSparse、TransA、TransG、KG2E 等模型。
- TransE 没有有效利用实体和关系的描述信息、类别信息,也不能处理互联网文本等非结构化信息,难以实现多元信息融合。代表工作包括 DKRL 模型等.
- TransE 孤立地学习每个三元组,不能很好地发现关系路径。代表工作包括 PTransE 等。
前景展望
- 不同知识类型的知识表示学习(树形、网格、一维、有向等类型的知识)
- 多元信息融合的知识表示学习(非结构化知识、多知识库知识、知识库其他信息)
- 复杂推理模式的知识表示学习(利用关系路径、三元组间复杂关系)